Expected Value Blackjack

3/31/2022 admin

Expected Value Blackjack 6,4/10 2903 votes

The part of the card that matters when playing Blackjack is its number value. For the actual numbered cards, you can gather that their card value is equal to the actual number they represent. Cards 2 through 10, no matter the suit, represent that number. Face cards, whether it’s. So for example, if you join a blackjack table with a 1.00% house edge, bet $10 per hand, and play about 60 hands per hour, your action would amount to $600 per hour. Respectively, you are expected to lose $6 on average to the house over the course of time.

Blackjack Expected Value Table
Expected Value Blackjack
Ace Blackjack Value
Expected Value Blackjack Calculator

Blackjack probability is just like any other probability in the casino. It’s a means of measuring the likelihood of certain events. You’ll often see probabilities expressed as percentages, but they can be expressed as fractions or odds, too.

Blackjack statistics is a way of measuring your actual results and comparing them to your predicted results. In the long run, your actual results will start to resemble your predicted results. But in the short run, random chance will ensure that anything can happen.

That’s why some players have huge losing streaks, while others have big winning streaks. The casino doesn’t worry about this, because they’ve set up the games and the payouts in such a way that they’re ensured a profit in the long run. That’s a matter of expected value.

Some Definitions Related to Probability and Expected Value

In fact, that’s probably the best way to introduce this blog post—with some definitions of some terms related to blackjack probability in general. That way you’ll be able to dig deeper into the main points of the post below.

Let’s start with the phrase “probability.” The word has 2 meanings. The first is that probability is the branch of mathematics that deals with the likelihood of an event occurring. The 2^nd is more useful—probability also refers to an event’s likelihood.

Probability is measured numerically, and an event’s probability is always a number between 0 and 1. An event with a probability of 0 will never happen. An event with a probability of 1 will always happen.

An event with a probability of 50% will happen half the time, on average. 50% is one of the more common ways to express that probability, but you could also say that this event has a probability of 1/2 and still be correct. Another useful way to express probability is in odds format. That’s when you compare the number of ways something can’t happen with the number of ways it can happen. With a 50% probability, an event has “even odds,” or 1 to 1 odds.

Expressing probabilities as odds can be useful when trying to decide whether you have an edge or not. In most casinos, the games all have a built-in edge, but blackjack is exceptional in this respect. I’ll get into that a little later in this post.

Another important concept in gambling probability to understand is the concept of “expected value.” This is what a bet is “worth.” A bet’s expected value can be positive or negative, but if you’re a player in a casino, it’s almost always negative. The formula for expected value is simple, too:

You multiply the probability of winning by the amount you stand to win. You also multiply the probability of losing by the amount you stand to lose. You subtract one from the other, and you have the expected value of the bet.

For example, if you have a 50% chance of winning $1, and you also have a 50% chance of losing $1, you have an expected value of 0. That bet is a break-even bet; over time, you won’t win any money at it or lose any money at it.

But let’s say you have a 45% chance of winning $1, and you have a 55% chance of losing $1. Now your expected value looks quite different:

+$0.45 – $0.55 = -$0.10

This means that over time you’ll lose 10 cents every time you make this bet.

Almost all casino game bets have a negative expected value. You’ll either lose more often than you’ll win, or you’ll win too little when you win to break even, or some combination of these factors. That’s how casinos stay in business.

That’s also why gamblers walk away a winner. In the scenario outlined above, you can’t lose 10 cents on a single bet or even a series of 2 or 3 bets. You’re going to win or lose $1 on each hand.

The expected value is an average expected over the long run.

And the long run is longer than most people think.

That’s why the casino can afford to pay winners occasionally and still make a huge net profit overall.

“The house edge” is another way of looking at the expected value of a bet, but it’s only used to describe bets where the casino has an edge over the player.

How the Casino Wins Consistently at Blackjack

You would think that the casino would have no edge in a game like blackjack. After all, the dealer is getting the same cards as the players. He has the same probability of being dealt a blackjack or going bust as a player.

The amazing thing about the house edge in casino games is that it’s usually a simple byproduct of the rules used by the casino for the game. For example, in roulette, the house gets an edge by paying off all the bets as if the 0 and the 00 weren’t on the wheel.

In blackjack, the house gets its edge by making the players resolve their actions and bets first before the dealer acts. In other words, you must make all your playing decisions before the dealer ever acts. This means that if you bust (get a total of 22 or higher), you automatically lose your bet—even if the dealer also goes bust. Since you acted first, and the dealer resolved your bust before having to play, the house has an advantage.’

This is a huge advantage made bigger by the fact that some players don’t play their hands optimally from a mathematical standpoint. In many cases, the best play is to stand on a hand which isn’t likely to win unless the dealer busts. A lot of players have trouble with this.

This advantage is so big for the casino that it can even afford to offer an extra high payout on some hands. In most casinos, a 2-card hand totaling 21 (a “blackjack” or “natural”) pays off at 3 to 2 odds. This means if you bet $100 and get a blackjack, you win $150.

The casinos can afford this bonus payout and still have a profitable mathematical edge over the player. This 3 to 2 payout is one of the reasons that smart players can get an edge over the casino, and I’ll have more to say about that later in this post.

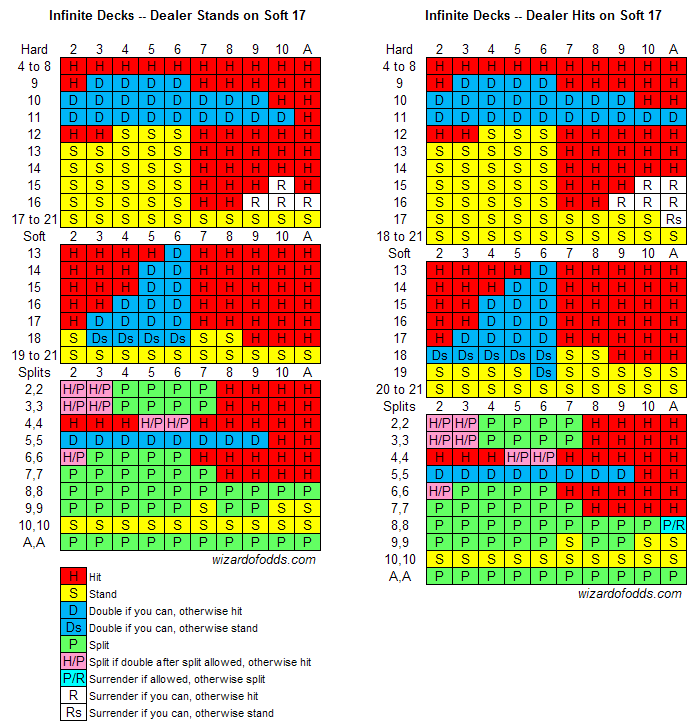
Since there a finite number of cards in a blackjack deck, it’s possible to calculate the mathematically best play in every situation. This is called “basic strategy.” Computer programs analyze the potential results of every possible decision in every possible situation. The move with the highest expected value is the correct playing decision.

The average blackjack player loses an average of 5% of every bet he places at the blackjack table. The average blackjack player is playing with “common sense,” “hunches,” or just pure dumb instinct.

The smart blackjack player, though, memorizes and uses basic strategy in every situation. This reduces the house edge to less than 1%. Depending on the rules variations in effect at a specific blackjack table, the house edge might be significantly less than 0.5%.

But it doesn’t matter how low the house edge is. If the house has an edge over the player, if the player gambles long enough, he’ll eventually lose all his money. That’s how the casinos stay in business.

Blackjack, though, is different from almost every other game in the casino. It’s a game where a smart player with the right strategy can get an edge over the casino. This is beyond the abilities of most players, and even a lot of players who THINK they’re playing with an edge over the casino are mistaken.

I talk about why and how that is in the next section.

How Probability in Blackjack Differs from Probability in Other Casino Games

The reason a strategic player can get an edge in blackjack is because as each card gets dealt, the composition of the deck as a whole changes. In any random shuffle of a 52-card deck, the cards might fall in any given pattern. But sometimes higher-value cards and lower-value cards are dispersed in the deck unevenly.

When I say “higher-value cards,” I means 10s and aces. Since these are the only cards that can create a blackjack—and the corresponding 3 to 2 payout—it’s better for the player if there are a relatively large number of these cards left in the deck.

“Lower-value cards,” on the other hand, increase your probability of going bust when you take a hit. They also make it harder to hit your 3 to 2 payout on the blackjack. If a deck has a relatively higher percentage of lower-value cards in it, the casino has a bigger edge than usual.

This might seem obvious, but think about it this way if it still isn’t clear:

You’re playing blackjack, and over the course of the 1^st couple of hands, all 4 of the aces are dealt.

What is the probability of being dealt a natural after this?

Since you need a 10 AND an ace to get a natural, your probability of getting a natural drops to 0.

Here’s another way to think about it:

When you’re playing roulette or craps, the odds are the same on every outcome. That’s because the number of possible outcomes on a roulette wheel don’t change. You always have 38 numbers with an equal probability of coming up.

When you’re playing craps, those 2 dice have the same number of sides (6) every time you roll them.

You don’t eliminate a number from the roulette wheel once a ball has landed in that slot. You start over on the next spin.

You don’t eliminate a number from the sides of the dice just because it came up on the previous roll.

But when a card gets dealt in blackjack, it’s gone from the deck until the deck gets re-shuffled.

That changes the probabilities on every hand.

How You Can Use This Information to Get an Edge over the Casino in Blackjack

If you could bet more when the deck has a higher ratio of 10s and aces and bet less when it doesn’t, you could get an edge over the casino. You’d be putting more money into action when you’re more likely to get a 3 to 2 payout.

And as it turns out, you CAN do exactly that.

You’ve probably heard of “card counting.”

Unless you’ve read about it before, you probably think it’s beyond the capabilities of most mere mortals. Maybe you saw Rain Man as a teenager and think you need to be able to memorize every card as it’s played to succeed in counting cards.

But the truth is, anyone who can add and subtract 1 can count cards. Maintaining the level of concentration of keeping that count accurate while not looking like you’re counting is the real trick.

You don’t track specific cards when you’re counting cards in blackjack. You just track the ratio of high cards to low cards. You assign a value of -1 to the 10s and aces, for example. Then you assign a value of +1 to the 2s, 3s, 4s, 5s, and 6s. The 7, 8, and 9 have a 0 value each.

When the running count is positive you bet more. The higher the count, the more you bet.

When the running count is 0, you bet less.

By doing this, you get a mathematical edge over the casino.

You can also use the count to inform your basic strategy decisions. Basic strategy assumes a full 52-card deck, but once the ratios of cards change as the deck gets depleted, the playing decision with the highest expected value can change.

This can increase your edge over the house even further.

You don’t gain a huge edge over the casino through card counting, though. You usually wind up with an edge over the casino that’s close to the edge the casino has over the basic strategy players.

This means that you might be playing with an edge over the casino of 0.5% or 1%.

That’s not a huge edge.

But it’s big enough.

Projecting Hourly Win Rates, Loss Rates, and Bankroll Requirements

How much does the average blackjack player lose per hour?

The formula is simple:

It’s the number of bets per hour, multiplied by the average size of those bets, multiplied by the house edge.

At an average blackjack player, you might see 80 hands per hour. Say you’re betting an average of $5 per hand, and you’re not using basic strategy, you’re looking at $400 in action per hour and losing 5% of that–$20/hour.

A basic strategy player, on the other hand, might reduce the house edge of 0.5%. This reduces his hourly loss rate to just $2/hour.

A card counter might be operating with a 1% edge over the house though. At the stakes we’re talking about, he’s winning $4/hour.

But consider this:

He’s raising the size of his bets based on the count, so his average bet size won’t be $5. It’ll probably be closer to $20.

Now we’re looking at $16/hour.

That’s not a great living, by the way. You can probably make the same money working at an In N Out Burger, in fact.

But as your bankroll grows, so does the average size of your bets. The people making real money counting cards might be putting $100 per hand into action on average. That’s $8000 per hour, or $80/hour in winnings.

$80/hour is some real money.

But one thing card counters need to think about is something called “risk of ruin.”

Remember how I talked about short term variance, and how you can’t expect long term expectations to hold true in the short term?

Just because you have an edge when counting cards doesn’t mean you’re going to show winnings every hour. You’re going to have wild swings of luck. That 1% edge is an average over thousands of hands.

You need a big enough bankroll to handle those swings in fortune without going broke.

The bigger your bankroll, the less likely you are to go broke before your edge and the long term kicks in.

This probability is called “risk of ruin.”

The most conservative approach is to have 1000 units to bet with. If you’re averaging $100 bets, you need a bankroll of $100,000 to play. If you have that kind of bankroll, your risk of ruin is just 1%.

On the other hand, if your tolerance for risk is better than that, you could get away with a much smaller bankroll—maybe 200 units. You’d still need $20,000, but you’d be able to play at that level. Your risk of ruin goes way up, though—to 40%.

I suggest to Texas holdem players that they know they’re good enough to move up in level when they can increase their bankroll to the appropriate amount for that new level. I think this recommendation holds true for blackjack players, too.

If you have $2000, you should be playing for an average of $10/hand. If you’re succeeding at that level, you’ll eventually have a bankroll of $4000, and you can move up to $20/hand, and so on.

How conservative or aggressive you are is up to you and your temperament.

Conclusion

Blackjack probability is a fascinating subject with no end of subtopics you can discuss. I could just as easily have written about the probability of going bust with certain tables as I did with the approach I took. I just thought it would be more useful to tackle the subject of blackjack statistics from an aerial view.

Most people, frankly, aren’t cut out to be card counters. It sounds easier in theory than it is in practice. Blackjack in most casinos is fast-paced and confusing, especially if you’re new to the game. It’s hard to keep up with those numbers in your head without looking like you’re paying too much attention.

And don’t forget that part:

The casino is watching for card counters. To say they frown on counting cards is an understatement. Casinos will risk throwing out players they could profit from if they suspect them of counting cards.

In fact, I think most casinos would be better off if they lightened up on card counters. I know plenty of would-be card counters who make enough consistent mistakes that they only THINK they’re playing with an edge over the casino.

My guess is that the number of would-be card counters who are profitable in the long run make up between 5% and 10% of the total number of card counters in the business.

At any rate, knowing something about the probabilities behind the game makes it more fun, even if you have no interest in being an advantage player.

And if you’re not an advantage player, fun’s what it’s all about. Comparing the cost of that fun to the amount of enjoyment you get from playing is what smart recreational gambling is all about.

Blackjack Expected Value Table

Please enable JavaScript to view the comments powered by Disqus.